Bentuk kisi yang dapat mendifraksikan elektron yaitu kisi yang memiliki keteraturan dan tersusun secara periodik, seperti halnya kisi pada kristal. Berkas sinar monokromatik yang jatuh pada sebuah kristal akan dihamburkan ke segala arah, akan tetapi karena keteraturan letak atom-atom, pada arah tertentu gelombang hambur itu akan berinterferensi konstruktif sedangkan yang lainnya berinterferensi destruktif. Syarat terjadinya difraksi adalah apabila panjang gelombang sinar sama dengan lebar celah/kisi difraksi.
Seperti yang telah kita ketahui sebelumnya, bahwa perilaku gelombang ditunjukkan oleh beberapa gejala fisis, seperti interferensi dan difraksi. Namun manifestasi gelombang yang tidak mempunyai analogi dalam perilaku partikel newtonian adalah gejala difraksi.
Pada tahun 1927 Davisson dan Germer di Amerika Serikat dan G. P. Thompson di Inggris secara bebas meyakinkan hipotesis de Broglie dengan menunjukkan berkas elektron terdifraksi bila berkas itu dihamburkan oleh kisi atom yang teratur dari suatu kristal.
Davisson dan Germer mempelajari elektron yang terhambur oleh kristal dengan menggunakan peralatan seperti pada gambar 1. Energi elektron dalam berkas primer, sudut jatuhnya pada target, dan kedudukan detektor dapat diubah-ubah. Fisika klasik meramalkan bahwa elektron yang terhambur akan muncul dalam berbagai arah, dengan hanya sedikit kebergantungan dari intensitas terhadap sudut hambur dan lebih sedikit lagi dari energi elektron primer. Dengan memakai blok nikel sebagai target, Davisson dan Germer membuktikan ramalannya.
Gambar 1
Eksperimen Davisson – Germer
Hipotesis de Broglie mendorong tafsiran bahwa gelombang elektron didifraksikan oleh target sama seperti sinar X didifraksikan oleh bidang-bidang atom dalam kristal. Dari beberapa percobaan yang dilakukan pada akhirnya terbukti bahwa eksperimen Davisson dan Germer merupakan bukti langsung dari hipotesis de Broglie mengenai sifat gelombang benda bergerak.
Komplikasi lainnya timbul dari interferensi antara gelombang yang didifraksi oleh keluarga lain dari bidang Bragg yang membatasi terjadinya maksimum dan minimum yang menjadi hanya kombinasi tertentu dari energi elektron dan sudut datang sebagai pengganti dari setiap kombinasi yang memenuhi persamaan Bragg :
Turunan rumus difraksi Bragg
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiAzLnBgWzWh5hcrneGJHEPVxOWG1m7OsWzqMIs3NR-MXSQcgz6t4fUR7zD3ppQTWt_7kKZTWK8N7gILKbfTInsFBd7AIEs5IR8XSjfPDGs-BtYDNggFzFIgNWlw_sy_NVV1bcx6tobDy8/?imgmax=800) |
Gambar 2
Beda lintasan, D = AB + BC = d sin q + d sin q = 2d sin q
Syarat interferensi maksimum :
maka Rumus difraksi Bragg
2dhkl sin q = nl
Percobaan di atas juga dapat dijabarkan dalam gambar sederhana di bawah ini
![clip_image001[4] clip_image001[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjOXdCxlUtzQ_kjDQkDw4k7F2HWDhQEs5jYuigFr4RbULUOUMiXdrKnp4RxD6F-RW_-0aHBZAyJFqj6OoXNi2L0yWF1VwOBlHbfON0zAbM9fmwFPJ1bdT9cZsVT7WFl-IhHGkTNhdOx0MY/?imgmax=800) |
Rumus difraksi Bragg :
Karena q sangat kecil maka :
sehingga :


![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgBLQsITOZRtK-LZASFjICtJC6JfyZVKIbK4EtzTLMXTeAYJosGgHFptRuXssJ1KbCEvi7HS3BYFxZekGrE0HOYUkShLgOteFe1eI-4A2sJHVaEnzWhMP6MY2tjDd9PjUQbpk-CGvhgPps/?imgmax=800)

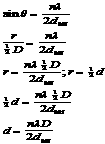



Tidak ada komentar:
Posting Komentar